Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Sierpinski-Dreieck
Das Sierpinski-Dreieck, 1915 von Waclaw Sierpinski beschrieben, ist ein sogenanntes Fraktal. Fraktale haben gebrochene Dimensionen, und für das Sierpinski-Dreieck gilt, dass es mehr als eine Linie, aber weniger als eine Fläche ist. Wie wir sehen werden, kommen noch andere Merkwürdigkeiten hinzu. Wollten Sie es zum Beispiel anmalen, benötigen Sie keine Farbe, da der Flächenanteil des Dreiecks gegen null strebt.
 Diese Abschnitte sollten erst durchgearbeitet werden, nachdem das Chaos-Spiel in Java programmiert wurde.
Diese Abschnitte sollten erst durchgearbeitet werden, nachdem das Chaos-Spiel in Java programmiert wurde.
Konstruktionsprinzip
Es gibt eine Reihe von Möglichkeiten, das Sierpinski-Dreieck zu erzeugen. Eine Variante, das sogenannte Chaos-Spiel, befindet sich im Java-Abschnitt (eine weitere interessante Konstruktionsmöglichkeit ergibt sich, wenn man Zellularautomaten zu Hilfe nimmt).
Alle Möglichkeiten stimmen darin überein, dass das Sierpinski-Dreieck die Menge der Punkte der Ebene ist, die übrigbleiben, wenn man die Verfahren unendlich oft wiederholt (iteriert).
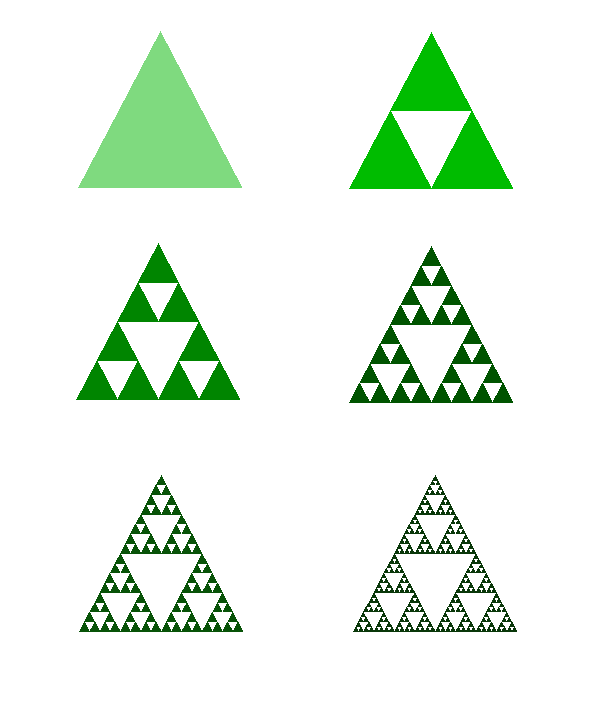
Mit zunehmender Iterationsfiefe (hellgrün → dunkelgrün) wird das Sierpinski-Dreieck immer besser erkennbar. Hier wurden fünf Iterationen dargestellt.
 Schauen Sie sich die Grafik so lange an, bis Sie ein mögliches Konstruktionsprinzip erkennen und erklären können.
Schauen Sie sich die Grafik so lange an, bis Sie ein mögliches Konstruktionsprinzip erkennen und erklären können.
Flächeninhalt - Umfang - Dimension
Im weiteren werden drei wichtige Eigenschaften des Dreieck aufgezeigt:
- Flächeninhalt
- Der Flächeninhalt ist null, d.h. um es auszumalen wird keine Farbe benötigt.
- Umfang
- Der Umfang ist unendlich. Niemand kann in endlicher Zeit um das Dreieck wandern.
- Dimension
- Die Dimension ist D=1,5850 und damit größer als eine Linie (D=1) und kleiner als eine Fläche (D=2).
Flächeninhalt
- a ist die Kantenlänge des Dreiecks
- n ist der n-te Iterationsschritt. Angefangen wird mit n=0 (Ausgangsdreieck)