Neuronale Netze sind künstliche Systeme, die die Arbeits- und Funktionsweise des menschlichen Gehirns zum Vorbild haben. Der Begriff Neuron stammt aus dem Griechischen und bedeutet in etwa Nerv.

Viele solcher Neurone bilden nun ein neuronales Netz. Im menschlichen Gehirn sind es ca. $10^{11}$ (100 Milliarden) Neurone.

Die Animation wurde von meinen Schülern Frederic Florian und Dennis Brodersen mit Gimp erstellt.

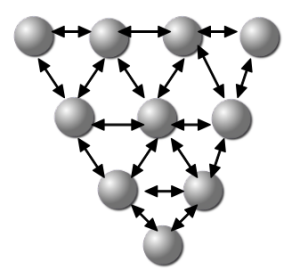
Neuronale Netze sind informationsverarbeitende Systeme, die grundsätzlich aus zwei Einheiten bestehen.

• Neurone
• Verbindungen

Die Neurone stehen durch die Verbindungen (auch Gewichte genannt) miteinander in Wechselwirkung. Die Gesamtleistung eines neuronalen Netzes hängt wesentlich von der Zahl und Gewichtung dieser Verbindungen ab. Das „Geheimnis“ zur Arbeits- und Funktionsweise dieser Systeme steckt in den Gewichtungen. Die Neurone können sich in zwei verschiedenen Zuständen befinden.

• Neurone können aktiv sein - man spricht davon, dass das Neuron feuert.
• Neurone können inaktiv sein (ruhend).

Diese künstlichen neuronalen Netze können eine Vielzahl von Aufgaben lösen. Um die Funktionsweise zu verstehen, müssen wir allerdings ein wenig weiter ausholen.

Ein neuronales Netz - die Neuronen (Nervenzellen) sind über Synapsen miteinander verbunden.	Das gleiche Netzwerk nun aber in einer schematischen Darstellung. Anstelle von Neuronen (Nervenzellen) sind nur noch Kreise gezeichnet. Die Verbindungen zwischen den Neuronen sind durch Pfeile gekennzeichnet.

1. Neurone
2. Verbindungen (Gewichte)
3. Netzeingabe (Abkürzung: net)
4. Aktivierungsfunktion
5. Updateregel (Update-Rule)

Wir bezeichnen Neurone mit $x_i$ oder mit $x_j$, um anzudeuten, dass es sich um verschiedene Neurone handelt. Neurone können innerhalb des Netzwerks verschiedene Aufgaben haben:

• Eingabeneurone,
• Ausgabeneurone
• oder versteckte Einheiten (hidden units), wenn sie weder direkt an der Eingabe noch an der Ausgabe beteiligt sind.

Wenn zwei Neurone gegeben sind, z.B. $x_i$ und $x_j$, bezeichnen wir mit $w_{ij}$ die Verbindung (Gewicht) zwischen dem Neuron $x_i$ und dem Neuron $x_j$. Wenn das Neuron $x_j$ ebenfalls mit dem Neuron $x_i$ verbunden ist, lautet das Gewicht demnach $w_{ji}$. Dieses Gewicht ist eine reelle Zahl und soll die Verbindungsstärke zwischen den Neuronen repräsentieren. $w_{ij} = 0$ bedeutet z.B., dass es zwischen den Neuronen $x_i$ und $x_j$ überhaupt keine Verbindung gibt.

\begin{equation} W=\begin{pmatrix} w_{11} & w_{12} & w_{13} & w_{14} & w_{15} & w_{16} & w_{17} & w_{18} & w_{19} \\\ w_{21} & w_{22} & w_{23} & w_{24} & w_{25} & w_{26} & w_{27} & w_{28} & w_{29}\\\ w_{31} & w_{32} & w_{33} & w_{34} & w_{35} & w_{36} & w_{37} & w_{38} & w_{39}\\\ w_{41} & w_{42} & w_{43} & w_{44} & w_{45} & w_{46} & w_{47} & w_{48} & w_{49}\\\ w_{51} & w_{52} & w_{53} & w_{54} & w_{55} & w_{56} & w_{57} & w_{58} & w_{59}\\\ w_{61} & w_{62} & w_{63} & w_{64} & w_{65} & w_{66} & w_{67} & w_{68} & w_{69}\\\ w_{71} & w_{72} & w_{73} & w_{74} & w_{75} & w_{76} & w_{77} & w_{78} & w_{79}\\\ w_{81} & w_{82} & w_{83} & w_{84} & w_{85} & w_{86} & w_{87} & w_{88} & w_{89} \\\ w_{91} & w_{92} & w_{93} & w_{94} & w_{95} & w_{96} & w_{97} & w_{98} & w_{99} \end{pmatrix} \end{equation}

Diese Gewichte kann man in Form einer Matrix $W$ anordnen. Im Beispiel oben sind 9 Zeilen und 9 Spalten also eine Matrix vom Typ 9×9 zu sehen. Die Eingabevektoren (Muster) für dieses Netzwerk haben damit 9 Komponenten.

• Der erste Index ist der Zeilenindex.
• Der zweite Index ist der Spaltenindex.

So befindet sich z.B. in der 4. Zeile und 6. Spalte das Element $w_{46}$.

Die nächste Komponente ist die Netzeingabefunktion $net_j$. Dabei ist $net_j$ eine Zahl, die die gesamte Eingabe für das Neuron $x_j$ repräsentiert. Die Eingabe hängt von allen Neuronen ab, die mit diesem Neuron verbundenen sind.

\begin{equation} net_j = \sum w_{ij} \cdot x_i \end{equation}

Gleichung 2 bedeutet, dass die gewichtete Summe des Neurons $x_j$ berechnet werden soll. Dabei werden alle Neurone, die Verbindungen zum Neuron $x_j$ haben, d.h., für die gilt $w_{ij}$ ≠ 0, mit ihrem Gewicht multipliziert und addiert.

Alle Netze benötigen die sogenannte Aktivierungsfunktion (siehe Abschnitt Aktivierungsfunktion). Die Aktivierungsfunktion bestimmt, ob ein Neuron, das über Verbindung mit anderen Neuronen Informationen erhält, feuern soll oder nicht.

Wenn der nächste Zustand der Neurone unabhängig von den anderen Neuronen berechnet wird, wird dies als sequenziell bezeichnet.

Dem steht die parallele Berechnung gegenüber, bei der alle Neurone gleichzeitig ihren Zustand ändern. Regeln, die beschreiben, wie man den Zustand der Neurone im nächsten Zeitschritt berechnet, nennt man allgemein Updateregeln.

Warren McCulloch und Walter Pitts beschrieben bereits 1943 eines der ersten Modelle für künstliche Neurone. Wir gehen hier nicht auf Details dieses Modells ein, stattdessen wollen wir ein Beispiel geben, wie die oben erwähnten Komponenten eines neuronalen Netzwerkes zusammenarbeiten, um ein konkretes Problem zu lösen.

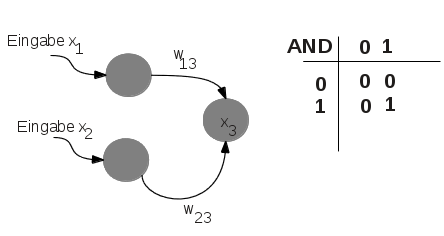
• Eingangsneurone ($X_1,X_2$) können 0 oder 1 sein.
• Ausgangsneuron ($X_3$) kann 0 oder 1 sein.
• Die Aktivierungsfunktion braucht für die Lösung dieses speziellen Problems nicht berücksichtigt werden. Ansonsten ist eine einfache Schwellenwertfunktion ausreichend.

Gegeben sind zwei Eingangsneuronen $X_1$​ und $X_2$​, sowie das Ausgangsneuron $X_3$​. Als Gewichte stehen $w_{13}$​ und $w_{23}$​ zur Verfügung. Das Ziel ist es, die Gewichte so zu belegen, dass die Wahrheitstafel für das AND-Problem erfüllt ist. Haben Sie eine Idee?

Das obige Beispiel hat anhand der AND-Funktion demonstriert, wie ein neuronales Netz diese Aufgabe lösen kann. Allerdings war dies ein sehr einfaches Beispiel, und die Gewichte waren zudem vorgegeben.

Ein Rezept dafür, wie viele Neuronen man nehmen muss und wie sie angeordnet sein sollten, um das Problem möglichst elegant zu lösen, gibt es übrigens auch noch nicht.